Deep Understanding of Content Areas
Introduction
When helping students develop a deep understanding of content area it is important to focus on conceptual understanding in mathematics. Procedural fluency is the foundation for students to be able to develop conceptual understanding so they are able to spend their energy on higher order thinking. The following pieces of evidence demonstrate different instructional strategies used in my classroom to deepen understanding of content areas.
Procedural Application
As mentioned in the Implementation of Instructional Strategies section, fluency prepares students to deepen understanding and free cognitive space for higher-level thinking without being taxed with procedural skills. I rely on students' fluency to engage all learners in developing higher order questioning skills and metacognitive processes. We do this through procedural application. Below is an example of this. In this problem, students were required to use a number of skills with manipulating decimals.



Shown to the left is an example of student work from real-world problems that required students to utilize fluency in multiple decimal operations. As seen in the first student exemplar her procedural competency in multiplying and adding decimals allowed her to demonstrate higher level thinking problem-solving skills. The second student exemplar illustrates students cognitive thinking by creating a known and unknown chart and plan. While these problem-solving skills allowed her to identify the correct operations, her work in fluency allowed her to accurately solve this problem like the first student exemplar.
Modeling
As the end of elementary education, 5th-grade mathematics is a cumulative curriculum. Students are expected to apply a number of principles to solve complex, multi-step problems. Their ability to succeed at this level requires a deep understanding of the content area. Another strategy I use to establish a depth of mathematical conceptualization is through modeling. This strategy allows students to visualize how mathematics works. This demonstrates an understanding of cognitive processing that stimulates multiple learning styles.



In the two pieces of evidence above, students use modeling to solve for the quotient and product of fraction equations. The tape diagrams used in the first piece of student work illustrate how the total is divided into smaller pieces. By dividing the total into parts, students are able to count the quotient by tallying the total number of pieces created. The area model used in the second piece of student work illustrates how fractions are multiple by visually creating a common denominator and differentiating the product from the factors. This type of visualization has been beneficial to all students, particularly those who have weak foundational skills in mathematics.

While the first piece of evidence demonstrates how lower students are appropriately supported with modeling, it should also be noted how high students are able to use modeling as a second strategy. Building their skill set allows them to practice higher order thinking.
Inquiry-Based Activities
After students engage in fluency work, they begin to explore each lesson's objective through inquiry-based activities. Inquiry-based activities are lessons that allow students to grapple with the material prior to direct instruction. These activities require students to evaluate different problems using prior knowledge or developing new ideas about mathematics. This engages all learners in higher-order critical thinking skills. Additionally, by exploring the content prior to instruction students are more invested in their own learning. Often times my students are eager to identify the solution to the problem. Students know I will not provide assistance during this time, which immediately builds engagement in our discussion following.



In the example above, students use inquiry-based learning to explore the use of a protractor. In this lesson, students were shown a protractor and asked to create a 45 and 135-degree angle. Prior to fifth-grade students do not have experience with protractors but are familiar with the vocabulary terms - acute, obtuse and right angle. As the teacher, I anticipated students using this prior knowledge as a basis for deep content understanding. An exemplar of this is seen in the image below.
In the video above, this student demonstrates inquiry-based learning by lining up her baseline and identifying degrees on her protractor. Although we have not named the origin in our lesson, she already has a deep understanding of how to use a protractor by paying attention to details and working meticulously.
Chart the Error
As an effort to adapt instruction to the needs of students, I utilize the instructional strategy of chart the error lesson plans. This type of lesson present students with two pieces of student work to analyze and discuss in order to identify a misconception. The two pieces of student work illustrate the correct answer versus the most common response. An example is shown below.
Unit 9 Assessment Question 10
While looking at assessment data I am able to identify different trends in students. As a strategy to address these misconceptions, I prepare Chart the Error lessons for students to engage students in the assessment of their understanding and instruction to close gaps. Particularly in this question, students either multiplied (majority) or divided the two numbers they saw. Given that at least one student from each class came to the correct answer, this is an instructional strategy I am able to utilize so students are able to take control of their own learning and I am able to act as the facilitator.
Students begin the class by recalling the question and evaluating each student's response. After 2 minutes, an open discussion is facilitated where students vote on which student they believe is correct. After this initial vote, a representative of each student is called on to justify their response. Typically it is during this time that students are able to have an "Ah-ha" moment where they deduct their misconception. Once this is reached we take another vote and solidify our key point/write our criteria for success.

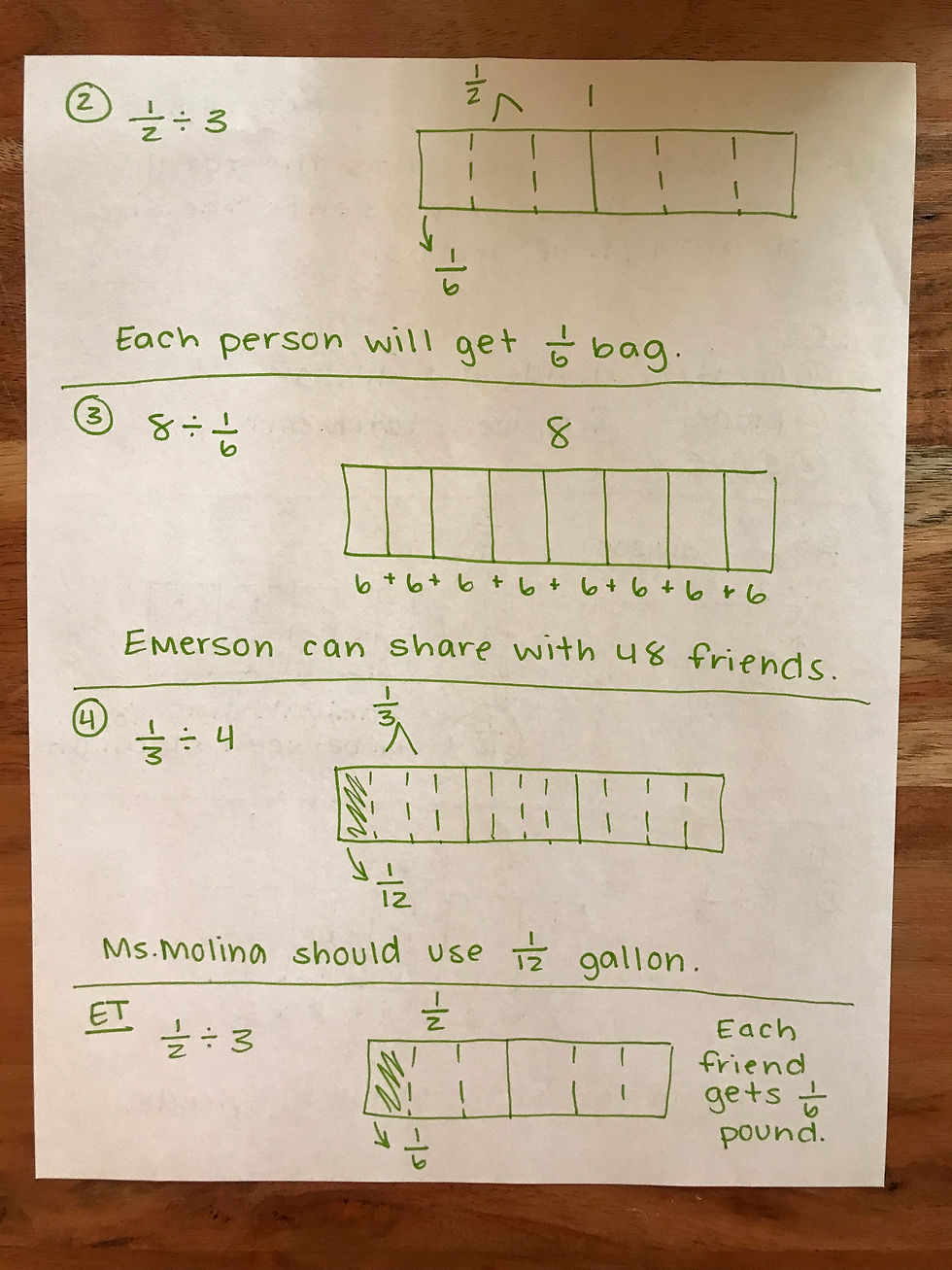




The artifacts above include a teacher exemplary piece of work versus two pieces of student work from this Chart the Error lesson. Both students have scratch paper that mocks mine in terms of note taking, however, the most notable piece of each student's work is their ability to correctly identify the dividend and divisor then correctly interpret their model. From this, it is apparent that Chart the Error lessons allow students to develop a deep understanding of content areas and build skills to apply knowledge in meaningful ways.
Conclusion
Throughout this section, I have highlighted the ways in which I strive to deepen understanding of content areas for students. These strategies include procedural application, modeling, inquiry-based activities, and chart the errors. With these activities ranging from critical thinking to conceptualization cognitive processes, I have provided student multiple models and representation of concepts and skills with opportunities for learners to demonstrate their knowledge through a variety of products. The result is that students are able to develop a holistic understanding of mathematics that will be transferable across content areas.