Qualitative Evidence
Introduction
Fifth-grade mathematics is the summative year of fundamental, elementary mathematics. There are a variety of skills students need to master to be prepared for the conceptual mathematics that is developed in grade six through twelve. One major skill is procedural multiplication using the standard algorithm. This skill allows students to multiply multi-digit numbers easily, which is necessary for the real-world multi-step problems in which students will need to rely on strong procedural skills and expand their critical thinking skills. Typically students have exposure to the standard algorithm in 4th grade; however, Achievement First's curriculum does not teach this skill until 5th grade. For this reason, it is critical that students rely on their conceptual understanding of numbers to build a strong fluency that is required for success on summative, high-stakes testing.
Multiplication Student Work with Rubrics
The Multiplication Yearly Progression outlines my intentional efforts to build students procedural and conceptual understanding of multiplication. To gain a better understanding this section will provide evidence of its application. As students progressed through the lessons of multiplication, benchmark assessments allowed students, and myself, to monitor their progress. In the evidence below, I have chosen three students to evaluated during each phase against the rubric. It should be noted that Student 1 in Phase I is the same as Student 1 in Phase II and Phase III. This evidence demonstrates the efficiency of the progression in developing students' conceptual and procedural understanding of multiplication using various forms. The ability to do this is pivotal for mastery of numbers and operation in base ten for grade 5.
Phase I: Multiplication using an area model
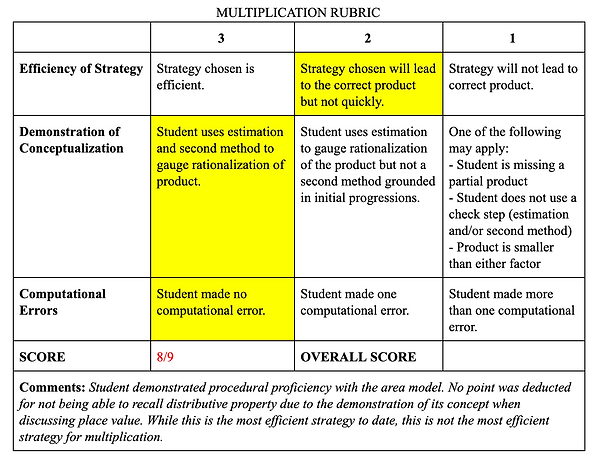
During Phase I of the multiplication progression, students are demonstrating their proficiency and understanding of the area model. As their teacher, I am looking closely at their understanding of place value and partial product as these are two conceptual understandings we will use to build fluency in the standard algorithm. Each piece of work was chosen to highlight specific progression. Student 1 demonstrated proficiency in using the area model but illuminates a common misconception in conceptual understanding of the distributive property. When this student accounts the distributive property to the number of "zeros", I am able to identify a need to go back to place value understanding and ground this in powers of 10. It will be important to show this student the difference between numbers with zeros versus numbers without. Student 2 demonstrated proficiency and conceptual understanding by being able to name distributive property and its association with place value to accurately solve the problem. Student 3 demonstrated proficiency and conceptual understanding by identifying place value and accurately solving the problem. While this student was unable to initially identify the distributive property as the mathematical strategy, their ability to identify place value shows me this is a vocabulary deficit rather than procedural or conceptual. All three students earned a 2 for Efficiency of Strategy because the area model is not the most efficient model. Receiving this type of feedback aims to keep students in inquisitive.
Student 1


Student 2


Student 3

Phase II: Multiplication with partial products
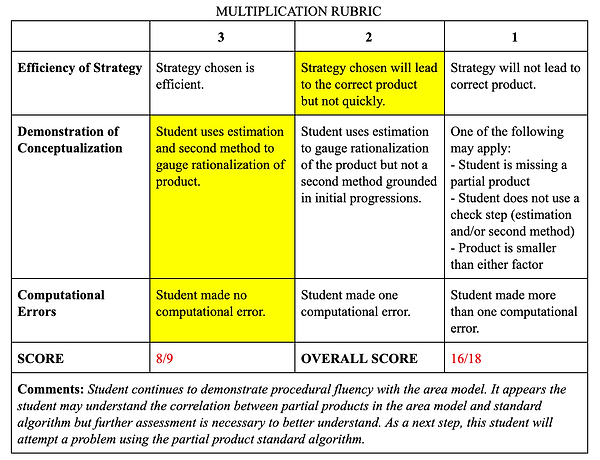
During Phase II, students use their conceptual understanding of the area model to use partial product standard algorithm. For this phase, it is important that students look at the factors as they do in the area model. For example, when multiplying 138 by 42. Students should be creating a list of partial products by solving (2x8) then (2x30) then (2x100). Being able to do this work without creating an area model is eliminating the need for students to write each step down thereby making the process more efficient. Student 1 continues to demonstrate proficiency with the area model but mistakes 40 for 4 in the second factors. Ignoring place value is a common misconception when transitioning from the area model to the standard algorithm. To address this misconception, I will create targeted questioning to demonstrate the importance of place value for students. Student 2 demonstrates proficiency with the area model as well as partial products. Student 2 is ready to transition to the most efficient form of the standard algorithm. Student 3 demonstrates proficiecny with the area model and partial products however it is suspected that this student may have copied the partial products from the area model to the standard algorithm. To confirm this misconception, I will assess this student's independent use of the standard algorithm. Similar to Phase I, all three students scored 2 for Efficiency of Strategy because neither the area model or partial product is the most efficient strategy. While effiency is the main goal of this progression, the main goal of this phase is to establish a connection between the area model and standard algorithm by looking at all partial products.
Student 1


Student 2


Student 3

Phase III: Multiplication using the standard algorithm
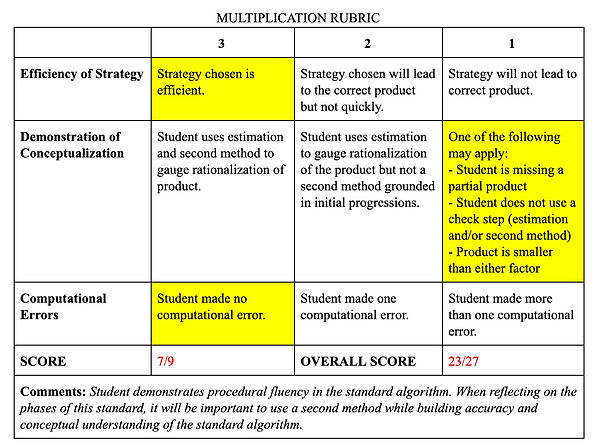
During Phase III, students demonstrate their understanding of the standard algorithm. While examining student work, I am looking carefully at a student's accuracy and use of a secondary method. In my class, it is important students are building the habit of checking their work with another strategy. Additionally, this habit will build students confidence as they become fluent with the standard algorithm. Student 1 demonstrates proficiency in the standard algorithm while using the partial product standard algorithm to check their work. Choosing the partial product standard algorithm as a secondary method demonstrated a conceptual understanding of the standard algorithm. Student 2 demonstrates proficiency in the standard algorithm while using the area model to check their work. For this student, they used the strategy they felt most confident with (area model) to check their work. It is important to highlight both Student 1 and Student 2 as effective strategies to encourage students to build their confidence authentically. Student 3 demonstrates proficiency in the standard algorithm but did not earn points for using a second method. Holding this student accountable for a second method demonstrates the importance of this skill.
Student 1


Student 2


Student 3

Conclusion
In this section, three students growth in one fifth grade standard is observed. All of these students demonstrated mastery of standard 5.NBT.B.5 by capitalizing on their procedural understanding of the area model to transition to fluency with the standard algorithm. This will be a valuable skill for students as they prepare for more higher-order thinking mathematics.